Lawmakers Needn’t Worry About Minnesota Conservative Energy Forum push polling
Center of the American Experiment has previously written about push polling conducted in 2018 by the Minnesota Conservative Energy Forum (MNCEF) which claims that 73 percent of Republicans and Independents in Minnesota “Believe Minnesota should pursue an all-of-the-above energy strategy and take action to accelerate the use of clean energy in Minnesota.”
Unfortunately, it appears this polling is being cited to pressure some members of the Minnesota Senate into supporting the proposed Clean Energy First legislation. While this bill contains some good provisions, it also contains some very bad provisions that would cause electricity prices to increase.
Furthermore, Center of the American Experiment’s more-recent polling shows these negative consequences are deeply unpopular among Democrats, Republicans, and Independents, alike, and lawmakers run the risk of facing potentially serious backlash if they vote for legislation that would increase the cost of energy in Minnesota.
First, a few words about polling in general
Polls are tricky things because they are highly dependent upon the public’s knowledge of a topic, and the wording of the poll questions.
Limited knowledge of the subject matter often results in people having favorable opinions of legislation, until they find out what it would cost, and how it would work. The best example of this is polling on Bernie Sanders’ Medicare for All (M4A) proposal.
The polling finds M4A is extremely popular, until poll respondents learned what it would cost and how it would work. In fact, support for M4A fell from 56 percent down to 40 percent after people learned the cost of the program, and support fell to 26 percent when respondents were told that M4A would cause some treatments and procedures to be delayed, as you cans see in the figure below.
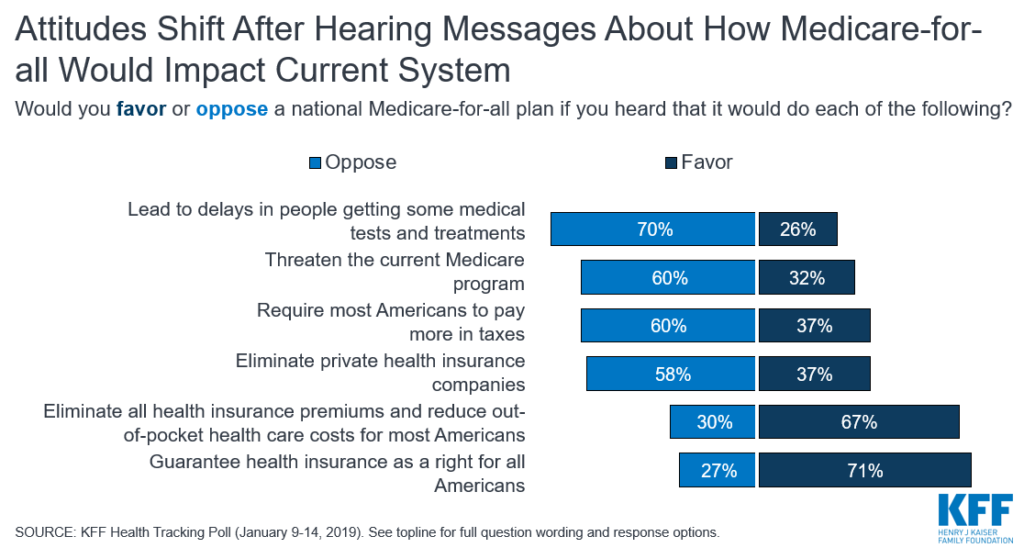
The graphic also demonstrates that the wording of poll questions is crucial. Poll questions can be easily manipulated to give survey takers the answers they want, rather than the answers survey respondents would normally give if the questions were presented in a more balanced way. Highlight the perceived benefits of a plan, get a positive response. Inform the public about the potential drawbacks of legislation, and support plummets.
Remember, push polls are designed to influence public opinion, rather than measure it. Groups often commission polls so they can use the results to pressure lawmakers into supporting their legislative agenda. So, let’s look at MNCEF’s poll question to see if it is even-handed, or if it appears to be seeking a predetermined outcome from their respondents.
MNCEF’s Poll Question
The respondents to the MNCEF poll were read the following statement:
“Minnesota should pursue an all-of-the-above energy strategy, which means lowering our heavy dependence on fossil fuels over time and allowing an increase in electricity generation from renewable energy sources as well as more energy efficiency, and I support taking action to accelerate the development and use of clean energy in Minnesota.”
According to MnCEF, 73 percent of Republicans and Independent voters agreed with this statement, and without the proper background information about Minnesota’s current energy needs, cost, or reliability, it isn’t surprising the statement received broad support.
Here are four reasons why conservative and independent voters probably agreed with the statement but wouldn’t if they had more information:
1) The phrase “Minnesota should pursue and all-of-the-above energy strategy” leaves the reader thinking Minnesota has an electricity shortfall when we actually have a surplus
If the state needed more electricity, maybe an “all-of-the-above” strategy would make sense, but Minnesota’s electricity demand has only grown by 15 percent since 2005, and we already have enough power plants to meet this demand.
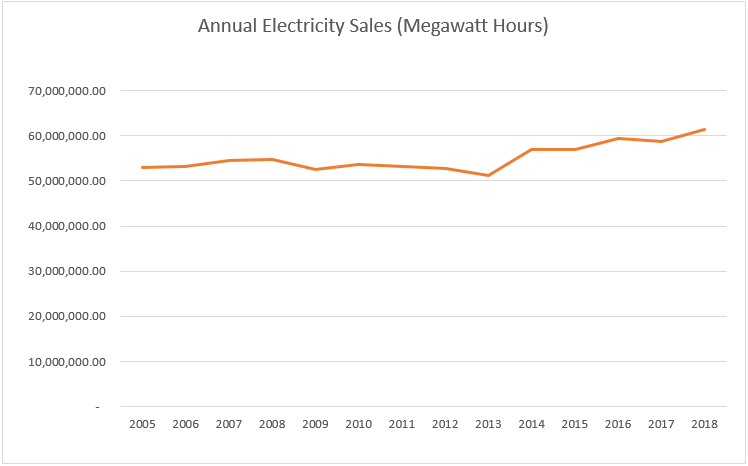
Since we already have enough power plants to meet demand, spending money on more power plants when they are not needed will result in higher electricity prices.
2) The poll question does not address costs
Building new power plants when we don’t have a need for the extra electricity has caused electricity prices to increase 27 percent faster than the national average since 2007, when Minnesota enacted it’s 25 percent renewable energy mandate, according to the U.S. Energy Information Administration (EIA).
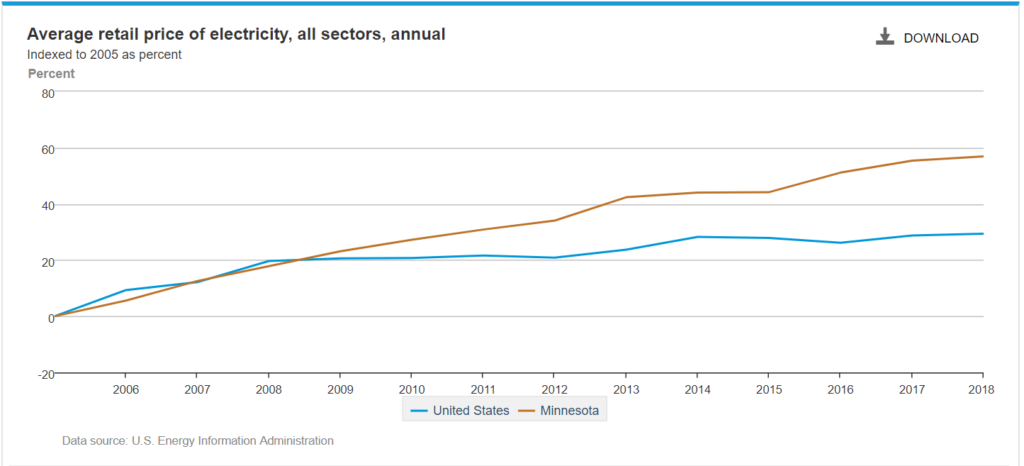
It’s important to remember prices would increase even in an “all-of-the-above” scenario because building new power plants increases costs regardless of whether the power plant is wind, solar, natural gas, nuclear, or coal. As I’ve often discussed, government-approved monopoly utility companies like Xcel Energy are guaranteed to make a profit on every dollar they spend on infrastructure, which gives them a powerful incentive to spend as much as possible.
These extra expenditures are paid by consumers in the form of higher electricity bills. EIA data show that Minnesota electricity bills already reached a new all-time high in 2018 as our state has spent more money on renewables, and this trend would continue if Clean Energy First allows utility companies to close their coal-fired power plants before the end of their useful lifetimes, and allows them to spend billions of dollars on new wind turbines, solar panels, transmission lines, and natural gas plants.
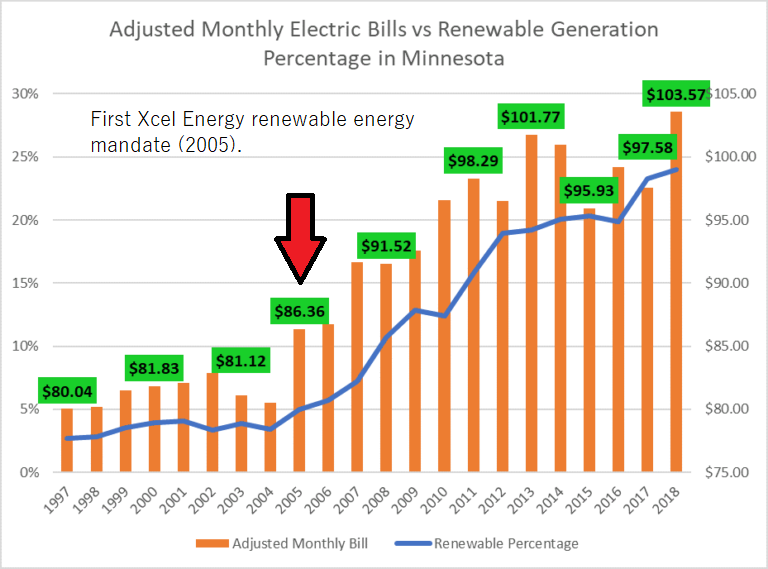
The fact that the MNCEF poll does not ask any questions about how willing people are to pay more for renewables represents a large flaw in their analysis. Center of the American Experiment’s polling of people living in Greater Minnesota shows 41 percent, a plurality, would not be willing to spend any additional money to reduce Minnesota’s impact on climate change, and this figure jumps to 62 percent of Republicans.
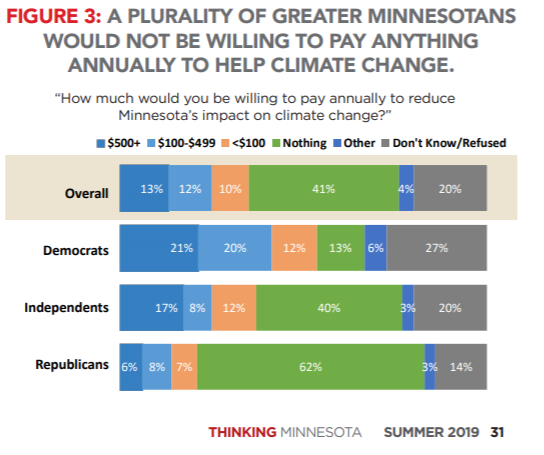
Center of the American Experiment’s research, Doubling Down on Failure, found that a grid powered with 50 percent renewable energy by 2030 would cost each Minnesota household $1,200 per year, every year through 2050. Democrats were the most likely to be willing to pay more than $500 per year at 21 percent, but only six percent of Republicans said they would be willing to pay more than $500 to avert carbon dioxide emissions to help reduce Minnesota’s impact on climate change.
These aren’t just our poll results, either. A recent poll by The Washington Post found 51 percent of Americans are unwilling to pay an extra $2 per month on their electric bills to fund climate policies, and 71 percent oppose paying an extra $10 per month.
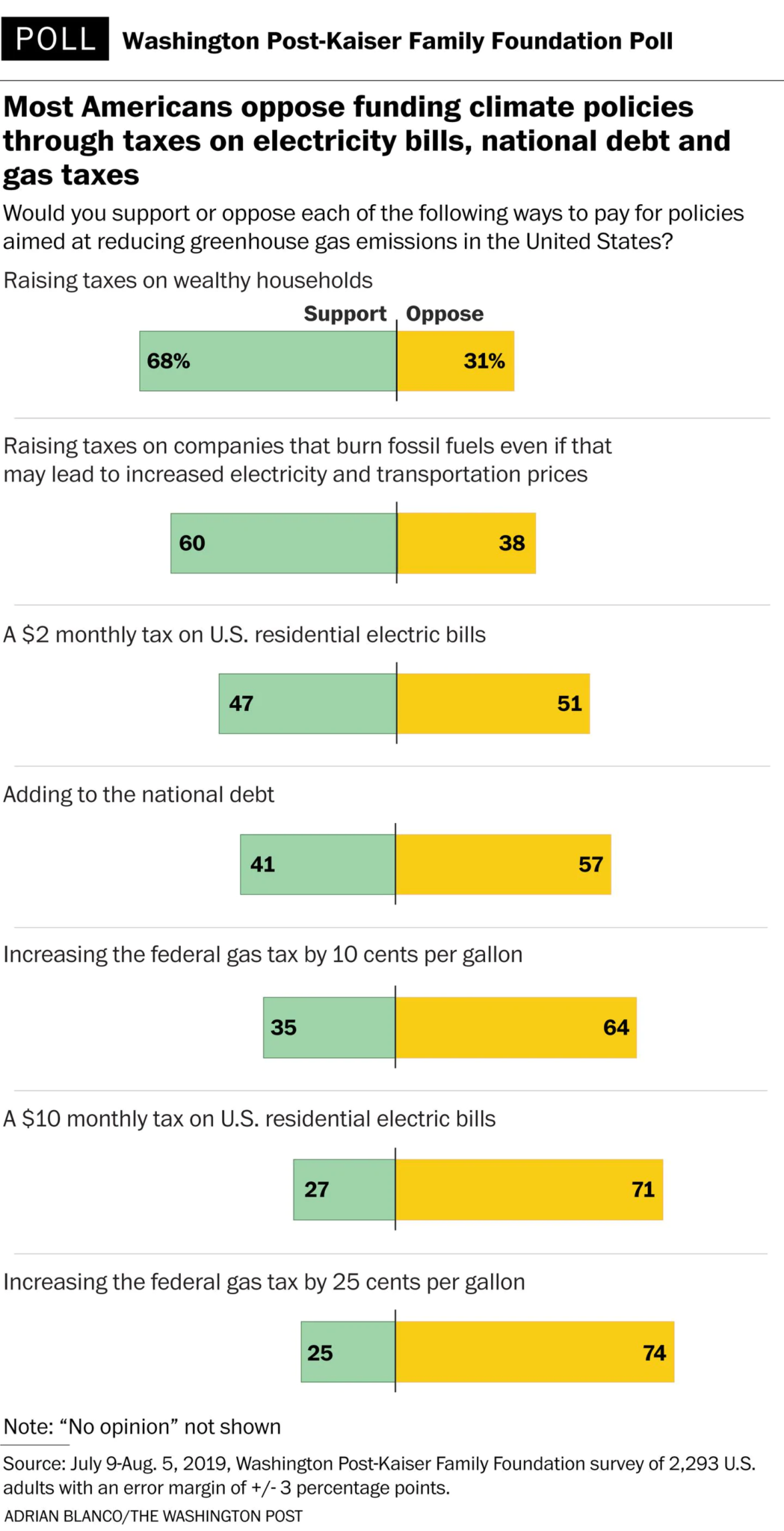
The main problem with polls is that they often ask people what they think about specific issues in a vacuum, but that’s not how life works. There are costs and benefits to everything, and it is important to weigh both when determining how we should proceed as a state on energy policy.
3) The phrase “lowering our heavy dependence on fossil fuels” hearkens back to the days of the Arab Oil Embargo and worries that the U.S. will soon run out of fossil fuels, but nothing could be further from the truth.
In fact, thanks to the fracking boom that has made the United States the largest producer of oil and natural gas in the world, the U.S. will export more energy than it imports by the year 2022, according to the U.S. Energy Information Administration.

The United States has more than 283 years worth of coal in the ground, enough natural gas to last for 90 years, and EIA estimates the United States will be a net exporter of oil until around 2050.
It would be interesting to see how Republicans and independents would feel about our use of fossil fuels if it was explained to them that these energy sources are abundant and will be produced in the United States for the foreseeable future.
4) The question makes it seem as if the government is not “allowing” renewable energy to flourish, when in reality renewable energy is only growing because of the government.
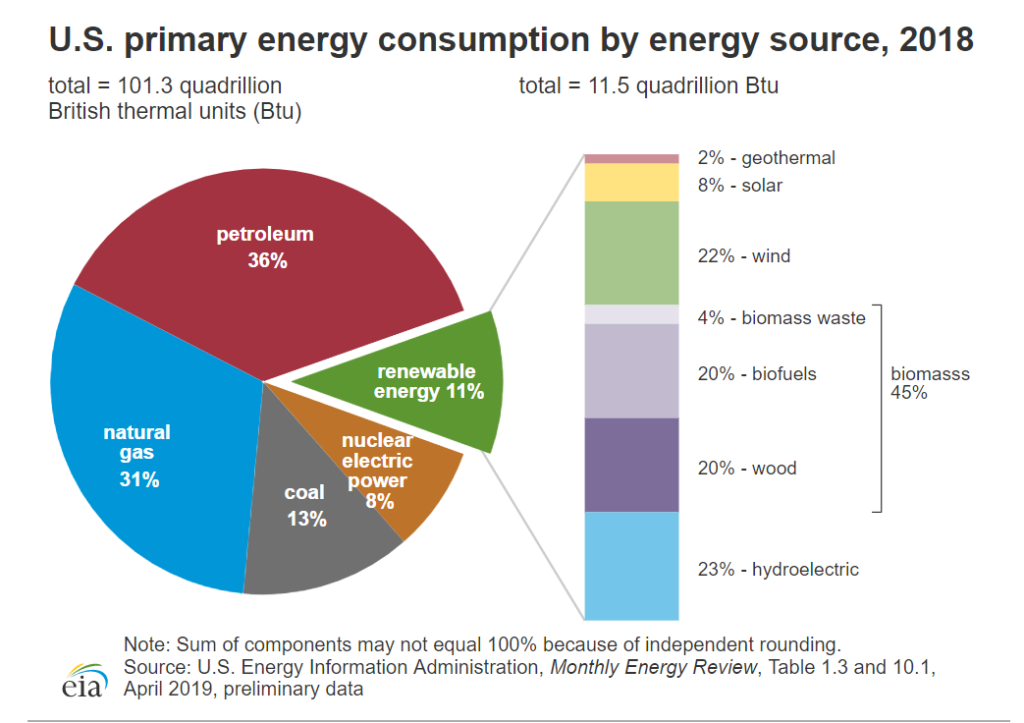
The chart below shows the use of each source of energy as part of our total energy consumption in the United States. Notice how fossil fuels make up 80 percent of our energy consumption, but wind and solar make up just 3.3 percent of our total energy use combined.
There are number of reasons for this, but chief among them is that wind and solar are simply more expensive and less dependable than other sources of energy like coal, natural gas, nuclear, or oil. This is why despite billions of dollars in federal subsidies for wind and solar power, they still produced less energy than hydroelectric dams in 2018.
It is safe to say that wind and solar would make up an even smaller portion of the pie if not for these subsidies. In fact, the graph below shows that wind and solar get far more federal subsidies than any other form of energy, and it isn’t even close.

The phrase “allowing an increase in electricity generation from renewable energy sources” is even more misleading because not only does the state of Minnesota “allow” renewable energy sources, it mandates them.
In fact, Minnesota’s Renewable Energy Standard is one of the most aggressive in the county, requiring utilities to provide 25 percent of their electrical generation from renewable sources by the year 2025.
So much for needing to “allow” more renewable energy to be built.
In conclusion:
Minnesota has already “taken action to accelerate the development and use of clean energy” and we have paid the dearly for it. We have spent more than $15 billion dollars on unneeded wind turbines and transmission lines and as a result we have lost our historical competitive advantage in terms of low electricity prices.
MNCEF may use conservative-sounding language and have pictures of Ronald Reagan on their website, but this poll leads me to believe the group was more interested in producing a headline they could use to pressure Republicans and independents into supporting the expansion of renewable energy programs rather than gauging public opinion in Minnesota.
Our own polling results show the findings of the MNCEF poll are a lot like Bernie’s Medicare For All, they crumple as soon as they touch the real world.
Additionally, energy posts are consistently the most engaging posts on our Facebook page. Based on the responses and comments that we get on our articles, I think there is a very real possibility that lawmakers would face backlash if they voted for legislation that would increase energy costs for Minnesotans, and I don’t think the results of a push poll merit this kind of risk taking.