MN Commerce Department Commissioner Kelley Tips His Hand: “Carbon Free” Still Means No New Nuclear
Yesterday, a reporter asked Governor Walz whether he thought Minnesota could meet his goal of generating 100 percent of our electricity from carbon-free sources without expanding nuclear power. The Governor deferred to Minnesota Commerce Commissioner Steve Kelley, who stated:
“We’re confident that by 2050 we’ll have the resources that we need to be 100 percent clean energy. Reliability has been a concern for a lot of people but we also anticipate there will be continued integration with a broader grid represented by the Midcontinent Independent Systems Operator, so reliability will come from the thousands of renewable energy generating facilities not just in Minnesota, but around the upper Midwest, so it seems to us that that is a doable goal.”
This statement is breathtaking because the theoretical possibility of using new nuclear power to achieve 100 percent “carbon free” electricity, rather than 100 percent “renewable” electricity, was the only nod to sanity Governor Walz had in his proposed energy policy, but it appears that was semantics without substance.
It appears the Governor fully intends to achieve his goals of reducing carbon dioxide emissions with renewable energy sources like wind and solar. This is problematic, because the Midcontinent Independent Systems Operator (MISO) has shown that the difficulty incurred from adding more renewables to the grid increases exponentially as penetration increases from 20 percent to 40 percent, and this becomes even more more difficult, and expensive, as penetration reaches higher levels, if it is even possible.
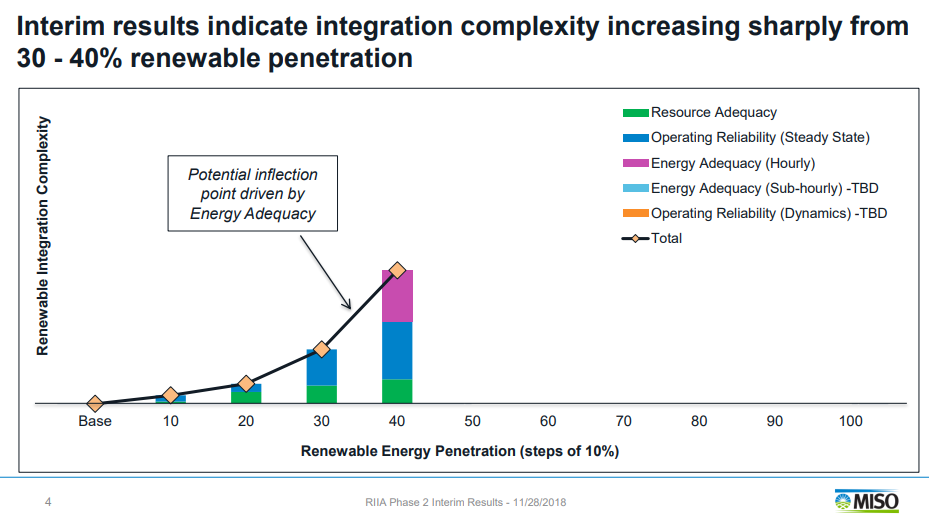
Renewable energy advocates are quick to resort to their new favorite refrain; that large-posteriored batteries can cure the intermittency that ails renewable energy sources like wind and solar, but research from MIT shows the cost of using batteries to provide baseload power increases the cost of electricity exponentially. Furthermore, the graph below assumes batteries will be three times less expensive than they are today.
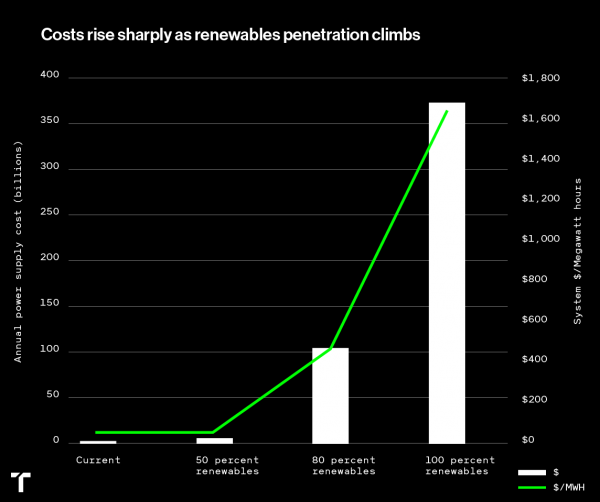
Just 24 hours of battery storage would cost Minnesota at least $133 billion, based on the Tesla battery that was installed in South Australia two years ago. An engineer I spoke to recently said Minnesota would need something along the lines of 700 hours of battery storage to integrate higher levels of intermittent renewable energy onto the grid. This would cost $3.78 trillion at today’s costs or “only” $1.26 trillion if we assume batteries cost a third less than they do today.
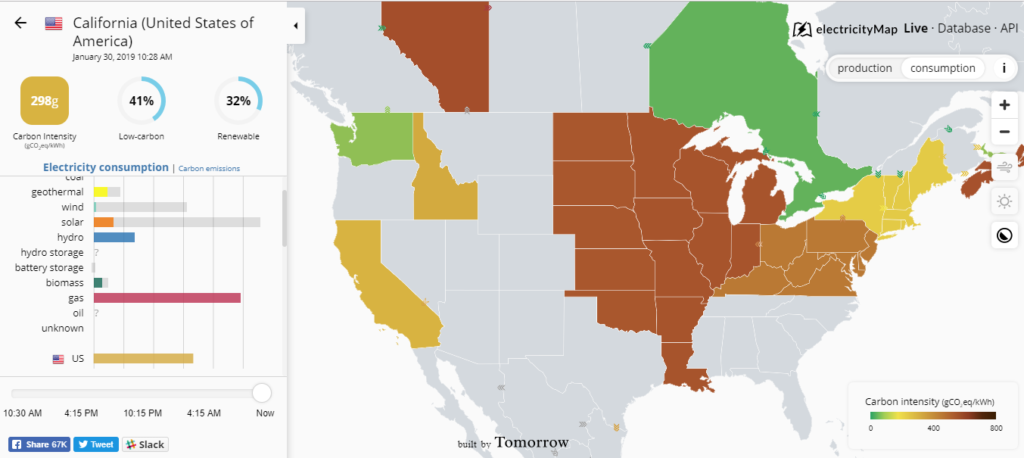
Furthermore, this idea that we could rely on thousands of renewable energy generators throughout the upper Midwest to provide reliable energy is purely a fantasy. Contrary to the claim that “the wind is always blowing, somewhere,” we clearly saw that the wind wasn’t blowing, anywhere, during the polar vortex which brought temperatures below -24 degrees F in Minnesota and caused wind turbines to shut down because it was too cold.
Reliability will not be ensured with thousands of renewable energy resources, it will be ensured with natural gas, enough natural gas to provide 100 percent of electricity demand in the event that the wind is not blowing or the sun is not shining. This results in thousands of megawatts of idle capacity on the electric grid which drives up costs.
Nuclear power, on the other hand, does not need backup generation because it is not dependent upon the wind or sun showing up to work. Capacity factors for nuclear power are around 90 percent. As we’ve seen from Lawrence Berkeley National Labs data, not a single wind farm in Minnesota operates above 50 percent, and only 13 percent of Minnesota’s wind capacity operated above 44 percent in 2017. What’s worse, we don’t even control when it is windy or sunny, so the capacity factors are even less relevant.
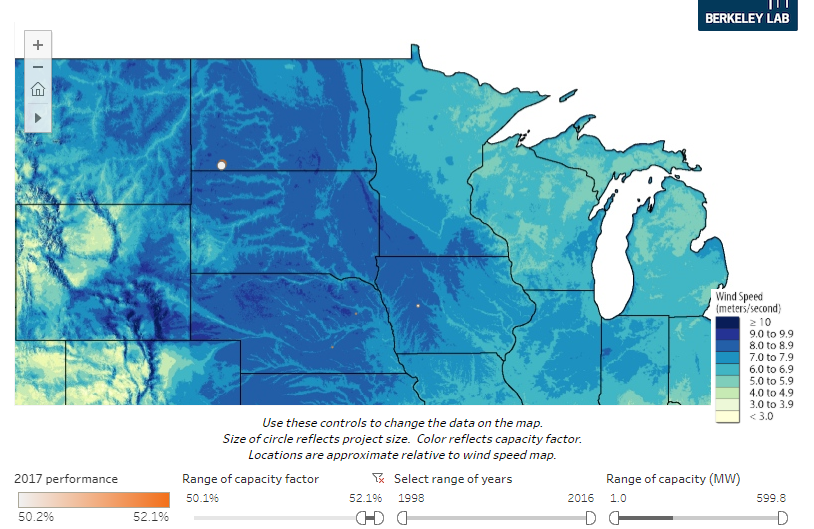
Furthermore, nuclear power plants last 40 to 80 years. Wind turbines are considered successful if they last for 20.
If Governor Walz really believes that climate change is an existential threat, why would he refuse to legalize the most reliable, affordable, and permanent source of electricity that does not emit carbon dioxide emissions? He wouldn’t. He would be hammering on legislators to legalize new nuclear power plants and looking for ways to build them in the most effective way possible.
The fact that is not even willing to advocate for repealing Minnesota’s ban on new nuclear power plants that has been in effect since 1994 means Governor Walz is not the adult in the room, no matter how me may try to position himself as the realist on environmental issues. It’s time for conservatives to take Governor Walz to task on his energy policy because he does not own the moral high ground, even though he thinks he does.