Grid Operators Confirm: Wind Didn’t Work During Polar Vortex
The energy world is buzzing today after the Midcontinent Independent Systems Operator (MISO) released a report stating the wind didn’t show up to work during the polar vortex that swept Minnesota on January 29 and 30. Electricity output from wind plummeted due to low wind speeds and because it was “too cold” for the wind turbines to operate.
That being said, why on Earth would DFL lawmakers in St. Paul propose legislation mandating more wind turbines?
Here are a few choice excerpts from media outlets covering the story with some of my own commentary sprinkled in.
From E&E News:
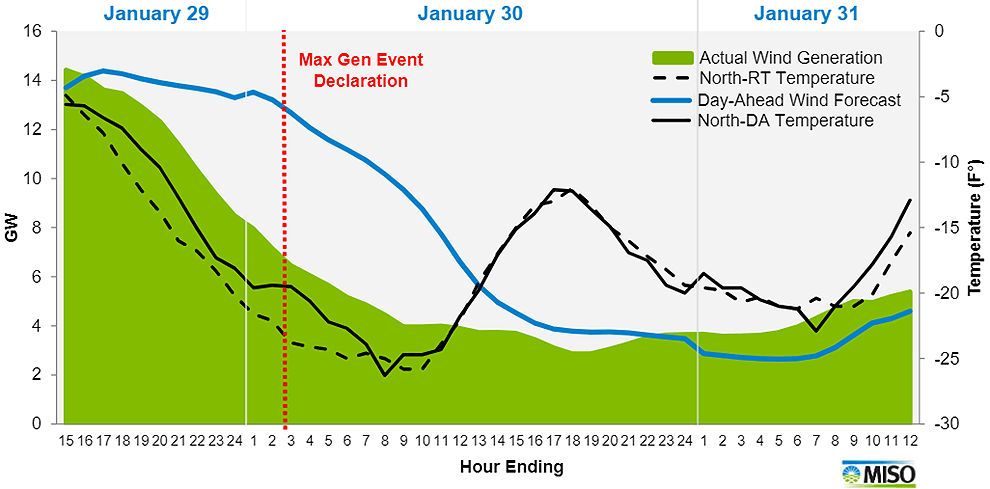
“As residents of the Twin Cities awoke on Jan. 29, the first of three straight days of subzero temperatures, about half of the region’s electricity was coming from wind farms dotting the Upper Midwest.
But grid operators would watch as electricity from wind steadily tailed off during the next day and a half.
By the evening of Jan. 30, there was less than 550 MW on the MISO North grid, supplying just 2.5 percent of the region’s power. The temperature, which had bottomed out an hour earlier, had fallen to minus 21 F with a minus 31 F wind chill.
Part of the reason for a drop in wind output was the normal daily variation in generation. In fact, the grid operator expected less wind energy to be available throughout Jan. 30, according to MISO’s day-ahead forecast.
Other turbines across the Upper Midwest shut down due to plunging temperatures.
Output from wind farms — a technology dubbed as the new baseload energy in the Upper Midwest — fell off even faster than anticipated starting the night before as temperatures fell below minus 20 F, the cutoff point below which turbines automatically quit operating.”
The new baseload? Give me a break. Wind will never be “baseload.” The reliability of the grid will be ensured with natural gas. Wind will be a supplement, at best, not a staple in our energy mix if we are foolish enough to rely upon it.
A MISO presentation released ahead of the committee meeting today shows that when the grid operator declared a “maximum generation event” just before 3 a.m. on Jan. 30, only about half of the almost 14,000-MW forecast of wind generation to be available was actually producing energy.
Brian Draxten, manager of resource planning for Otter Tail Power Co., said wind turbines across North Dakota shut down because of the extreme temperatures. In fact, he said the wind farms went from a power producer to a 2-MW load on its system because they required heat to avoid being damaged.
Xcel Energy Inc., which likewise gets nearly 20 percent of its energy from wind, said wind farms in Minnesota and North Dakota automatically shut down when the temperature reached minus 20 F.
So we’ve established that wind turbines generated far less electricity than they were expected to provide during the polar vortex, and they were a net drain on the electricity grid. So far, no good arguments for building more unreliable wind turbines.
Minnesota, in fact, is among the states where clean energy advocates are pushing a bill to establish an 80 percent renewable energy standard by 2035 with a goal of 100 percent clean energy by midcentury (Energywire, Feb. 6).
Clean energy advocates believe the intermittence of renewables doesn’t become an issue for grid reliability until penetration reaches about 75 percent.
Also read: “Clean energy advocates believe the rent seeking can continue for the foreseeable future.”
Thankfully, there are adults in the room who are exposing the idea of ever-increasing penetration of renewable energy sources as the irresponsible and dangerous idea that it is.
Wade Schauer, research director for Americas power and renewables research at Wood Mackenzie, noted that it gets “exponentially” harder economically to justify renewable penetration beyond 50 percent, including hydroelectricity, because of an increase in curtailments during periods of overproduction and because of a need for dispatchable power.
“You can keep building more, but you still need more backup generation to be there on days like these during the polar vortex,” he said.
MISO, too, published a renewable integration impact assessment last fall that said going beyond 40 percent renewable penetration will be increasingly challenging and could require additional transmission.
Ultimately, Schauer said significantly higher renewable penetration will depend on better long-term forecast accuracy for wind energy, more transmission and longer duration battery storage than is available today.
MISO data also show that coal and gas-fired plants were unavailable in the cold during the polar vortex, but it is unclear where these outages occurred. According to the Star Tribune, Xcel Energy did not report any outages at their coal or natural gas plants during the polar vortex.
Xcel’s wind turbines, however did not fare so well.
“Xcel, Minnesota’s largest electric utility, receives 21 percent of its generation from wind in Minnesota and the Dakotas, and its turbines automatically shut down around 20 below. They were generally down during the nights of Jan. 29 and 30, the company said in statement.”
Wind speeds were less than forecast on those days, meaning power production was less than expected. Ice on turbines hampered wind production. And then there was the brutally low temperature.
Wind turbines are often programmed to shut down when the thermometer is 20 below to 25 below because equipment can be damaged if turbines continue running. (The same is true during violent storms, when turbines are also programed to shut off at certain wind speeds.)
Renewable energy is a feel-good fad that does little to reduce our dependency on fossil fuels because we can’t depend on them to show up to work when we need them most. Increasing our reliance on wind and solar, rather than admitting that we made a mistake and changing course, would be a massive failure of leadership on the part of Minnesota lawmakers.